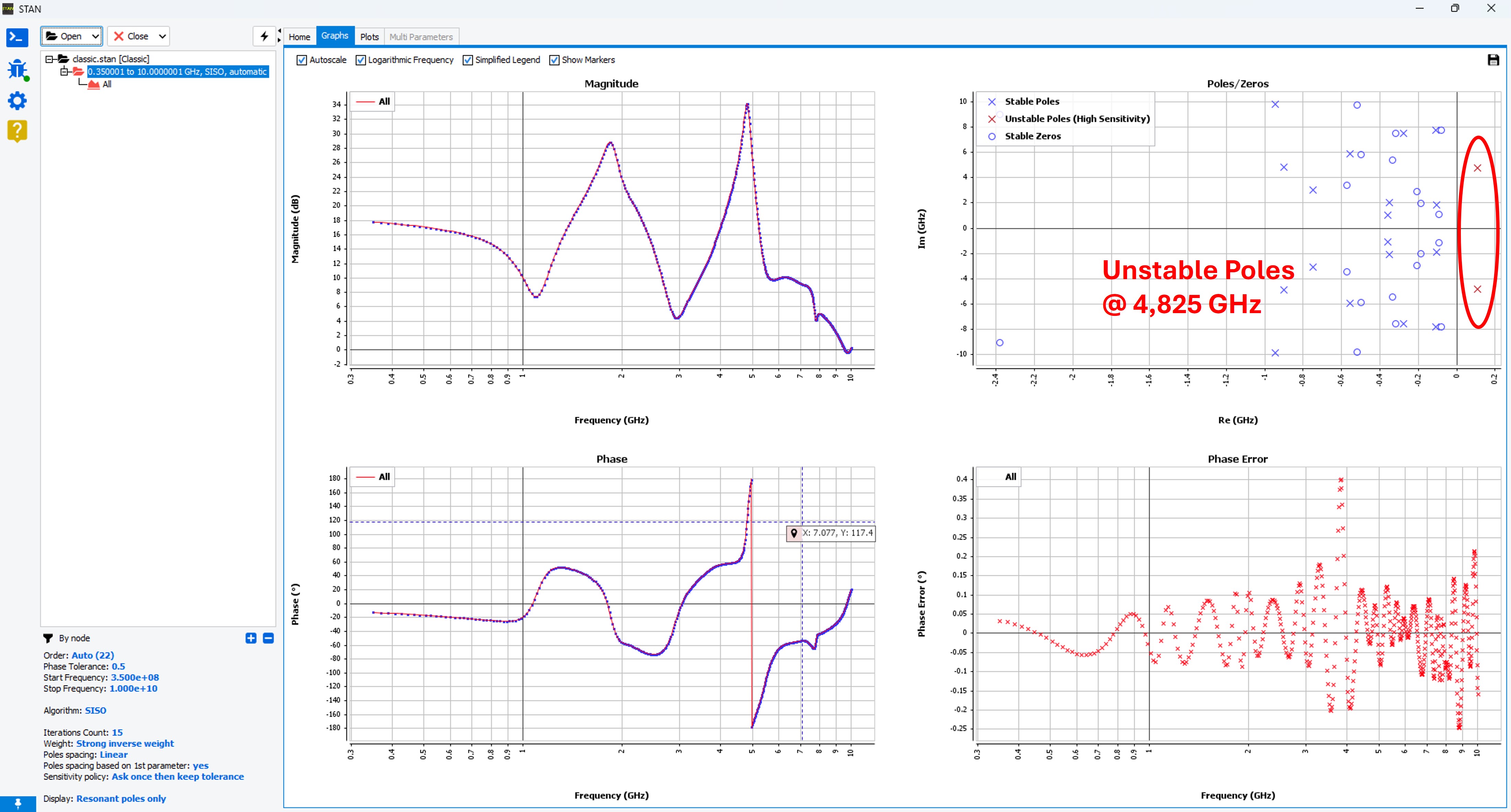
How to know if the steady state solution is unstable ?

If the poles obtained from the identification have a positive real part, there is an instability in the steady-state solution, Figure 1 & 2. The presence of a pair of unstable complex-conjugate poles means that an oscillation will start up at the frequency of the poles. This frequency is given by the imaginary part of the poles.