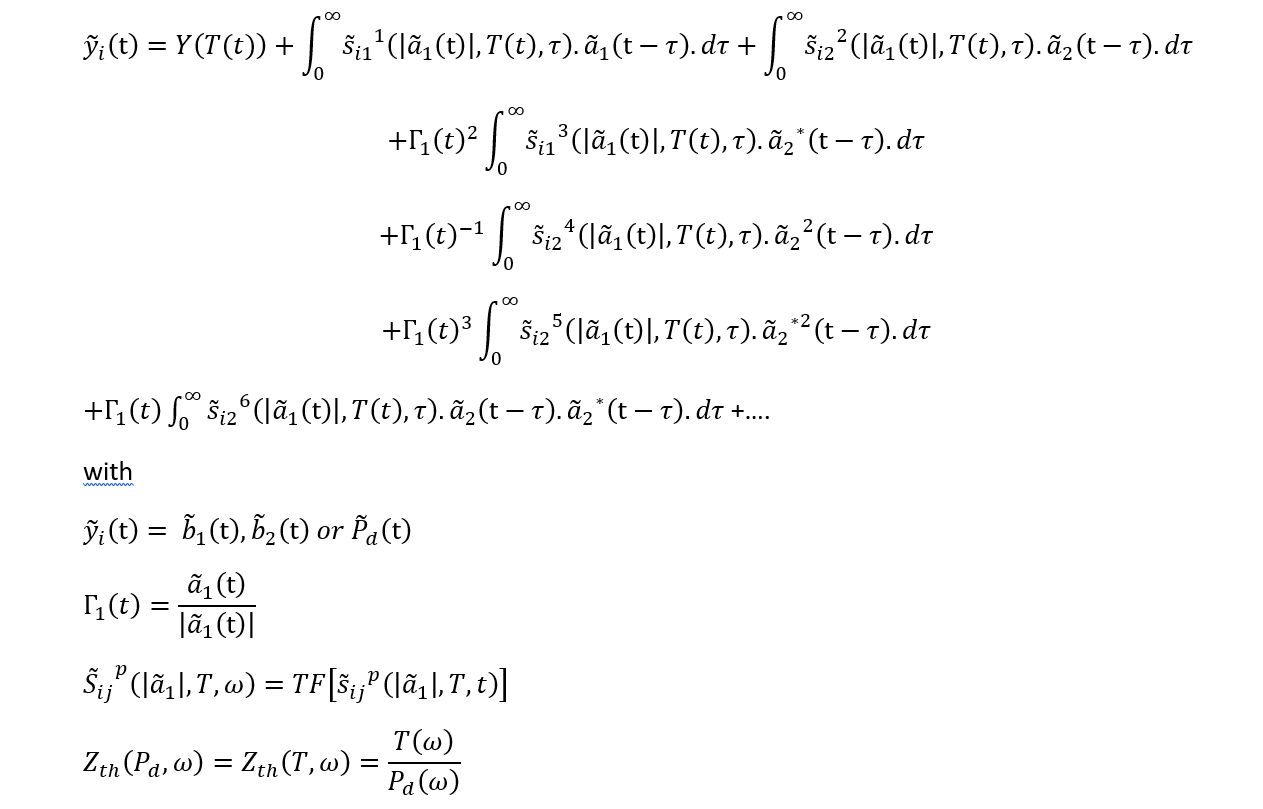B-HFTH model
Bilateral type model: i.e. that it takes into account the variation of the source and load impedances. This model can be reduced to a fixed load impedance model when measurements are provided only on 50 Ohm (or other optimal load impedance).
High Frequency Electric Memory Model: i.e. that it considers only the frequency dispersion caused in the operating band of the amplifier; it ignores the dispersion caused by the dynamics of the polarization circuit
Thermal model: ie. that it takes into account the effects of self-heating (by characterization or 3D thermal simulation of the thermal impedance)
Mathematical description.
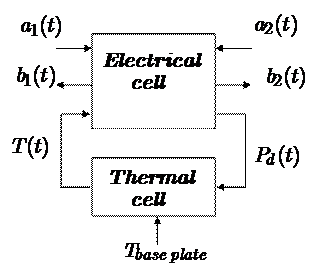
The principle of the model is based on a feedback structure of an electric model HPA-B-HF looped on a thermal cell as below:
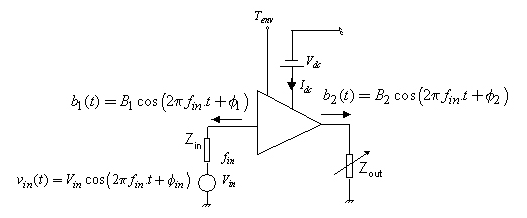
Pd represents the average dissipated power, T the temperature, a1, a2, b1, and b2 the incident and reflected waves at the accesses of the DUT.
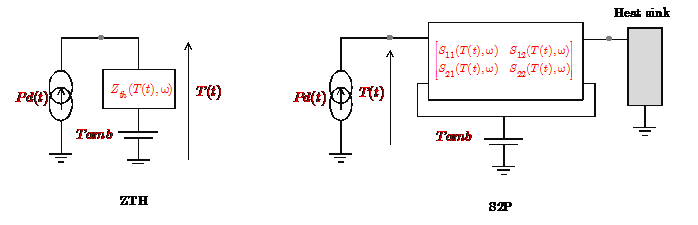
The thermal model is represented by an equivalent thermal impedance Zth making it possible to evaluate the variations in temperature within the system from the Pdiss.
The equations of the model are of the form below, where they are non-linear temperature dependent S parameters.
These parameters are measured in pulsed RF mode under isothermal measurement conditions. The extraction process of the electrical model consists in approximating the kernels in power (by Splines) and in frequency (Poles / Residues) to deduce the impulse responses.
The thermal impedance is also transformed into an equivalent thermal R / C network by poles / residues decomposition. As indicated above, the thermal impedance can be non-linear, ie, a function of the temperature or the dissipated power. The extraction process of the thermal model is based on a 3D thermal simulation followed by order reduction techniques allowing to obtain a reduced thermal model, in the form of a dipole impedance or a quadrupole impedance matrix. It is also possible to connect an external thermal network, to represent the flow of heat in the environment.
Identification principle.
The HPA-B-HFTH model is identified from the pulsed CW load-pull measurements. This corresponds roughly to a model HPA-B-HF parameterized in temperature.
The model is declined in several orders of bilaterality, ranging from 1 to 5. The greater the order, the more the model is able to take into account strong load mismatches in non-linear operating area. It takes a minimum of 3 load impedances to be able to identify the simplest bilateral model (order 1 or linear model),. 6 impedances for order 2 (quadratic model), 10 for order 3 (cubic model), 15 for order 4 and 21 for order 5. In practice order 3 seems sufficient to offer a good accuracy on all Smith's abacus. Higher orders tend to present numerical oscillations.
Input quantities :
Output quantities :
Validity domain.
The HPA-B-HF-TH model provides an excellent representation of the effects of self-heating and HF frequency dispersion. He ignores the dynamics of polarizations.